The Knot Untying Spectrum

I recently investigated a fun little problem in knot theory, about what kinds of knots can be generated by partially untying a more complex knot. I got some interesting results before realizing that somebody else had already asked and answered the same question. I still think it's a neat problem, so I'll explain the background and how I went about investigating it. It might be useful to have a knot table open in another tab while reading this, and I apologize in advance for the terrible MSPaint graphics.

Left: A DNA molecule with a knot at multiple stages of untying, getting a bit longer with a smaller knot at each stage. Scale bar is 8 microns. Right: Diagram of the pathways that a 101 knot can take to untie (we do not expect the knot in the left image to be a 101, it is just an example).

This was motivated by my recent paper that I talked about here. In it, we discussed observations of DNA knots that partially untied into smaller knots, implying the original knots were sufficiently complex for this to happen. We also ran numerical simulations of a 101 knot  untying, and found that it could either untie completely or in multiple stages, becoming an 81, 61, and 41 (figure-eight) before untying.

A knot unties in two stages at the right side of this stretched DNA molecule, leaving a smaller intermediate knot after the first stage. For what kinds of knot is this mathematically possible?

Even though we don't know what kinds of knots I'm actually studying in my experiments, we know from several. different. measures. that they are very big and complex (by knot standards), so I was envisioning a simulation project where we look at the pathways of many different kinds of knots untying in polymers to determine the statistics of knot untying mechanisms. However, I realized that there was a more fundamental problem, which is that it's not trivial to figure out what kind of knot you get when you partially untie a bigger knot. Sure from looking at a drawing of a 101 knot you can figure out that it goes to an 81 knot, but try to tell me what kind of knot you get when you partially untie a (let's say) 10165 knot. So, I wanted to figure out what kind of knots can untie into other kinds of knots. There are many, many knots, but limiting my knot menagerie to 10 crossings or fewer gave me 249 knots to study and seemed like a good cutoff because it was small enough that I could wrap my head around it but large enough that I could get statistics.

Partially untying a 10165 knot gives you a new knot of (initially) unknown topology.

Knots are represented by diagrams, which are a two-dimensional projection of a three-dimensional entangled loop, where one section of a loop can pass over or under another. A lot of knot theory has to do with how these diagrams can be transformed into one another, with certain moves keeping the topology of the same (called Reidemeister moves) and others leading to a different kind of knot. Knots are typically labelled in Alexander-Briggs notation, which has a big number for the minimum number of times the knot diagram crosses itself, and a smaller number for the index of that knot within the set of knots with that many crossings. There isn't much pattern to the index number, except that for even crossings the first one is a twist knot, and for odd crossings the first is a (P,2) torus knot and the second is a twist knot. There is no deterministic way to know the type of knot given its diagram, but there are calculations you can do with a given diagram (call it A) that can be compared to the same calculation from a diagram of known topology (call it B), which gives evidence that diagram A represents knot B, but knowing this for sure is an open mathematical problem.

The mystery knot with over a dozen crossings has the same Alexander polynomial as the trefoil knot, which provides evidence that is in fact a trefoil knot (it is!).

One such calculation involves calculating the Alexander polynomial, where you label all the n crossings in a diagram and the n+2 regions that the diagram divides the plane into, and define an (n × n+2) matrix with values determined by how each crossing behaves next to each region, and take the determinant of a square subset of the matrix (see a better explanation on page 21 of this document). There are similar polynomials called Jones and HOMFLY*, but I like Alexander the best because it's my name (and also it tends to yield simpler rational numbers). The Alexander polynomial is used a lot in polymer simulation papers, where the chain is projected onto a plane, the Alexander polynomial is calculated based on that projected diagram, and the value at some point is compared to the known values of specific knots, to try to determine what kind of knot it is. This works well if you have reason to believe that all your knots are simple (for example when forming in an equilibrium polymer), but breaks down if you have a more diverse set of knots. For example, the 61 knot has the same Alexander polynomial as the 946  knot, and there are 11-crossing knots with the same Alexander polynomial as the unknot (for which the polynomial is a constant 1).

So, based on what I knew about this, my procedure for figuring what kinds of knots I get when I partially untie a bigger knot would be something like:

1. Partially untie knot.
2. Calculate Alexander polynomial
3. Compare to Alexander table.
4. Profit.

The question is, what is the mathematical operation equivalent to "pulling some rope out of the knot just a little bit and stretching it again"? This comes back to how topology is defined in simulations of open chains (which technically are unknotted because they aren't a closed loop). To calculate the topology, the chain is looped through "minimally interfering closure," which, if the ends are far apart and knot is in the middle, just means connecting the ends at infinity.  But if I open a closed chain, untie it a bit, stretch the ends really far apart and then reconnect them, I can skip the last step and just close it immediately after untying. So, this open-untie-close operation is equivalent to taking one of the crossings in a diagram and changing it from "over" to "under" or vice versa, which is known in knot theory as a crossing switch. A topic of interest in knot theory is the unknotting number of a knot, which is the minimum number of these crossing switch operations that are required to untie a knot. One thing I like about this is that you can mentally picture the switch and then mentally schwoop out the now-non-essential parts of the knot to try to figure out how it evolves to a simpler knot. My mental schwooping only goes so far though.

The untie-and-pull operation of an open knot is better represented by the crossing-switch of a closed knot.

So all I had to do was take all 249** knot diagrams with 10 or fewer crossings, calculate the Alexander polynomial for each one, flip all 2,343 crossings, and calculate the Alexander polynomial for each new diagram. At this point it was clear that I should be doing this with some kind of algorithm, so I downloaded the knot theory package for Mathematica, which is maintained by a professor at the University of Toronto.

For each knot you can calculate something called a Dowker code (also known as Dowker-Thistlethwaite), which is an array of numbers representing the crossings of a knot diagram, with numbers that are positive if the crossing has the strand going over the other, and negative if it goes under. A crossing switch can be achieved simply by replacing the positive numbers with a negative or vice versa.

How to calculate a Dowker code. I can make it "untie" a little by switching one of the negative numbers to positive or vice versa.

So, I had my means of attacking this problem: iterate through every knot, iterate through every crossing, flip it, calculate the Alexander polynomial at some value, and save the results for later analysis. When I started doing this and looking at the results, one issue that arose was duplicates. I mentioned above that some pairs of knots have the same Alexander polynomial. For knots with 9 or fewer crossings, there were about a dozen of these pairs, many of which involve composite knots (two knots on the same closed loop), whose polynomials are the product of the prime knots that make them up. In many cases I was able to use the Jones polynomial to break the tie***, the one exception being the 912 knot, which has the same Alexander and Jones polynomials as the 41#52 compound knot. However, these duplicates were typically a nuisance but not an issue, because the duplicates typically had different crossing numbers and usually the lower one made sense but the higher one didn't (if I untie an 8 crossing knot and I get either a 6 crossing or a 9 crossing knot, I know it's the six crossing knot).

There are a few families of knots where it's simple to figure out what happens when they're partially untied. Twist knots, for example (like the 101, 81, 61, 41 in my first example) will untie into the unknot if their "clasp" is cross-switched, but will untie to a twist knot with two-fewer crossings if they are untied in their twisty section. Likewise, (P,2) torus knots will evolve into (P-2,2) torus knots when one of the crossings is flipped. I haven't been able to figure out a general principle for higher-order torus knots, although the simplest example (the 819 knot) can be partially untied into two trefoil knots as well as a 51 torus knot. It came as a surprise as me that a prime knot can be untied into a composite knot, although it makes sense when you look at the diagram.

Left: Highly symmetric (P,2) Torus knots can only untie into (P-2,2) torus knots. Right: The 819 knot can untie into two trefoil knots.

Most knots had multiple simpler knots they could untie into. At each crossing number, there was a distribution in the number of untying pathways that was approximately Gaussian. There was also a knot at each level that had the greatest number of untying pathways. More symmetric knots tend to have fewer pathways for intuitive reasons, the lowest being the (P,2) Torus knots that can only untie into (P-2,2). 62, 76, 814, 932 were all champions, while 10117, 10119, and 10147 all had eight untying pathways. There a few other things that can be done with this information, like looking at how the average number of pathways grows with the crossing number, or calculating the total number of knots that can be reached starting with a given one and untying it multiple times. I was somewhat interested in figuring out the greatest number of pathways that a given knot could take to untying, but never really got around to doing this. Another thing that might be interesting is to find the knot that must untie in the greatest number of stages (e.g. the 101 can take 4 steps to untie, but it can also take zero), however the answer this is probably just a (P,2) torus knot, which takes roughly P/2 steps to untie.

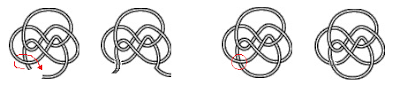
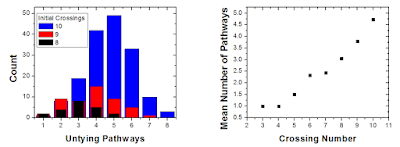
The 814 knot can untie in five different ways, and take 8 different paths to untie completely.

There was one result that I didn't understand, which is that apparently the 10161 knot could be untied into the 10145 knot. If this is real then there may be a family of knots that can be cross-flipped into knots with the same crossing number, if it's not real then there are flaws in my algorithm, but I can tell from known cases that it's not *totally* wrong.

Untying pathway stats with no real insight. Left: Histogram of the 8, 9, and 10 crossing knots and how many ways they can untie. Right: Average number of untying pathways as a function of crossing number. Is it linear?!

When breaking into a new field, it can be hard to do a proper literature review because you don't know the lingo. The closest thing I could find to what I was interested in was "knot adjacency," which was investigated by a few people who were interested in how knots were "n-adjacent" to the unknot, meaning they could be untied with a minimum n simultaneous crossing switches. However, after I got my results I did a bit more digging and found the term "Gordian distance," which lead me to a 2010 thesis that computed a table of "knot distance" between the prime and composite knots that I was investigating, all the knots that could be reached with a certain number of crossing switches from another knot. What I had done was essentially the one-flip subset of this. The application of this table was also DNA related, it was inspired by topoisomerase enzymes that can untie knots in DNA by passing strands through one-another. I was able to check my results against those in the table to verify I wasn't completely wrong in my conclusions.  A more recent paper, published in the Journal of Knot Theory and its Ramifications, spoke of knot fertility, defining parents and descendants based on crossing flips. They were interested in calculating the knots that can be cross-flipped into every single less complex knot. The most complex fertile knot they found was 76. There are definitely others interested in this problem, but there aren't enough of them that they've settled on a unified vocabulary.

I did go a bit further in some aspects than these other two papers, but I don't think that's enough to warrant a publication on it. One question that I think remains open and would be interesting if solved is to find a general form for the untying pathways of torus knots, beyond just the (P,2) variety. I have two data points for this: the 819 (the (4,3) torus knot), which can untie into either two trefoils, the 51 torus knot, or the 75 knot, and the 10124 knot ( (5,3) torus) which can be untied into 819, a compound 31#51, 942 and 947 (or their Alexander-sharers). Even from those two points there are patterns that emerge, but that's a bit too extrapolaty. Even though I wasn't the first to do this, it was still fun figuring it out.



*HOMFLY seems like a name a TV executive from the early 90s would make up for a rapper appearing on the show. However, it is named after the initials of six of its derivers.

**actually just 247 of them...the 31 and 41 knots obviously won't untie into anything smaller.

***no pun intended