I am not a particle physicist or a cosmologist but I would like to talk about a particle cosmology paper I read a while back that I found quite interesting and readable. It's an older paper, but I just started this blog.
The paper "How Stable is the Photon?" by Julian Heeck was published in Physical Review Letters (PRL), one of the top physics journals, in 2013. A free version can be found on arXiv. The first sentence of the abstract is "Yes, the photon." which suggested to me that it was going to be my kind of paper.
As far as we know, photons do not decay. This is related to the fact that light has no mass, and there's nothing it can decay into: heavier particles decay into lighter particles, but nothing is lighter than massless light. Heeck points out that the masslessness and stability of light need not only be assumptions, they can be tested empirically.
What would massive decaying light imply experimentally? The electrostatic interaction, that decays with a 1/r Coulomb potential, can be thought of as mediated by the exchange of virtual photons, and if those photons had mass and decayed, the force would fall more quickly (I believe it would be described as a Yukawa potential, which decays as e-r/r but I could be wrong here). So, one could do an experiment measuring the force between two charges at varying distance, plot a graph of force vs distance, and perform a power-law fit to measure if the exponent is consistent with -2 or not. If it isn't, that hints at a photon mass, and if it is, the error bars on that exponent put limits on the photon mass. A lot of physics doesn't ask the question "how big is this thing" but rather "how big could this thing be, and still not be detected by our experiment?" Williams et al. did a fancier version of this experiment, and found that the exponent is within 3x10-16of 2, or to write it out in a silly manner they found that the Coulomb force scaling exponent was between -1.99999999999999996 and -2.00000000000000027. This put a bound on the photon mass of less than 10-50 kg or 10-15 eV. More recent measurements push that down a few orders of magnitude, but needless to say the photon mass is very small, if it exists.
Theoretically, a photon mass implies that electromagnetism is described by the Proca rather than Maxwell equations. It also has the strange implication that light does not actually travel at the speed of light, which seems tautologically false. It would imply that the-speed-that-light-travels and the-speed-that-is-fixed-in-special-relativity are not the same, and that light now has a rest frame.
If light could decay, what would it decay into? Heeck mentions that, without introducing new particles beyond the Standard Model, it could decay into the lightest neutrino without violating what is known about their oscillations (which depend on the differences in mass between the three types). The upper bound of the sum of three masses is known (about 0.1 eV), but the lower bound and the breakdown of each mass are not known. In Heeck's decaying photon scenario, the photon can decay into two of the lightest neutrinos without violating conservation of energy. This decay would be very unlikely to occur, to which Heeck declares "Still, unmeasurable small SM [Standard Model] rates never stopped anyone from looking for a signal, as it would be a perfect sign for new physics."
So if photons had mass and could decay into neutrinos, how would we check if that were actually happening? Light is so light that it barely ever decays, and it's so fast that its lifetime would be extended further by time dilation. Heeck's solution is to look at the light that has been travelling the longest: the cosmic microwave background (CMB). Four hundred thousand years after the big bang, the universe became cool enough for hydrogen to form, which made it transparent to light. At the time, the gas in the universe was hot enough to emit visible thermal radiation, which and 13 billion years later some of that reaches the Earth from all directions, having been shifted into the microwave part of the spectrum by the expansion of the universe. The spectrum of the CMB is still consistent with thermal radiation (before the COBE satellite confirmed this in the 1990s, a number of PhD theses were written explaining why it was not thermal, or so my undergraduate relativity professor told me), and possible deviations from this could be signs of photon decay.
The bulk of the "theory" in Heeck's paper is a re-derivation of the Planck spectrum that includes the photon mass and the expansion of the universe. The new spectrum deviates from the classic Planck spectrum in the lower-energy part of the spectrum, where fewer photons are now expected (my understanding of the paper is that the Lorentz factor of the lower-energy photons is smaller, so the lifetime in the low-energy regime isn't as dilated). Heeck fits the CMB spectral data to his new equation with the mass and decay rate as free parameters. Unsurprisingly, he finds that both are consistent with zero. However, much like the deviations from 2 in the Coulomb exponent, fitting to the CMB data can put constraints on the photon lifetime. Heeck finds that if photons can decay, they must have a lifetime in their rest frame exceeding three years. Because they are going so fast, this is extended quadrillion times (1015) by time dilation, making their mean lifetime much longer than the age of the universe.
Heeck summarizes: "In conclusion, a massive photon sounds crazy and exotic, but it really is not. A massless photon is neither a
theoretical prediction nor a necessity, but rather a phenomenological curiosity." I liked this paper because it used a clever analysis to test something everybody had been taking for granted and gets a concrete result, and in general it was a pleasure to read and I learned a lot. Reading it makes me wish I knew more about particle physics so I could play around with stuff like this.
Monday, 31 August 2015
Sunday, 30 August 2015
Solving a Non-Existent Unsolved Problem: The Critical Brachistochrone
During my research I came across an obscure mathematical physics problem whose established answer was wrong. I attempted to solve this unsolved problem, and eventually found out that I was the one who was wrong.
As part of my paper on falling through the centre of the Earth, I studied something called the brachistochrone curve. From the Greek for "shortest time," this is the curve that allows something to fall from point A to point B in the least amount of time. Finding this shape was posed as a challenge by Johann Bernoulli in 1696 to the leading physicists of the day, and was quickly solved by Isaac Newton, Gottfried Leibniz, and others. The solution is a shape called a cycloid, the shape traced out by a rolling circle. Apparently Albert Einstein likes to ride them, and it is the fastest shape because it has the right balance of short distance and high speed (the cycloid with the green ball wins, ignore yellow and blue).
The brachistochrone curve inside the Earth (assuming uniform density) was worked out, among others, by Venezian around 1966. The problem is more complicated because gravity now varies (linearly) with distance from the centre, and the geometry is polar rather than Cartesian. The solution is the related hypocycloid, traced by a smaller circle rolling inside a bigger circle.
Another problem that had been worked out in the literature was the brachistochrone problem around a point-mass in Newtonian gravity: polar geometry where the gravitational field decays as 1/r2. This was solved independently by a few researchers, and there isn't an analytical solution (one that can be written down as an equation), but these curves generally run deeper than the hypocycloid, because gravity is comparatively stronger towards the centre, so they can save time by going deeper. What's interesting, however, is that if two points on the surface are separated by more than 120 degrees, no such curve exists. Beyond this, it is faster just to go "down" to the centre, switch directions, and go "up" to another point, rather than taking a smooth curve. If you try to calculate the brachistochrone curves, they hit a wall, so to speak. (that image is from John Gemmer, one of the people to figure this out. His website on the problem has some neat animations.)
Because the Earth is not uniform, and is not a point-mass, I developed a model to find the brachistochrone between any two points on a sphere, with an arbitrary gravitational field inside, which is where this story begins. Ultimately this model allowed me to calculate the brachistochrone through the realistic Earth, but that is not what this post is about.
I wrote a script that would generate these curves, going from their point of maximum depth to the surface. (For those that care, it is this equation, where alpha is -n and Rd is the deepest radius, 0.5 in the gif below. It is solved with the Euler method.)
As the starting point got deeper and deeper, the curves tended to get straighter, which makes sense: the fastest way through the centre of the Earth is a straight line.
However, if the gravitational field was sufficiently "sharp" (e.g. it increased strongly with decreasing radius), the straight paths would go up at an angle. I thought that this was just due to insufficient computational precision, but this was in fact the same phenomenon as the Newtonian critical brachistochrone: the path does not exist beyond a certain angle.
This is the case for a 1/r2 gravitational field, but what about other fields? In my second paper on planetary tunnels, I explored the dynamics through a sphere where the gravitational field depended on some radius with some arbitrary power, 1/rn, depending on the distribution of mass. If the mass was concentrated at the centre, n=2, and if it is uniformly distributed, n= -1, and I tried to describe our solar system with everything in between. So, I looked into this critical angle for different values of n. What I found was that the angle does depend on the field exponent, getting smaller (approaching vertical) as the field gets "softer" and bigger as the field gets "sharper." I had found a numerical relationship between the field exponent and the critical angle. At this point, it was time to look more closely at the literature to make sure I wasn't re-inventing the wheel.
It turns out, I was. Two publications had mentioned the power-dependence of this critical angle. One was by Kiwi NASA mathematician Gary Tee, who started working on problems like this after the Apollo missions. In a footnote of one of his papers , Tee mentioned that a coworker, Ron Keam, had shown that as a function of field exponent, the critical angle is 2π/(n+1), meaning that for n=2, the critical angle is 2π/3, 120 degrees as expected. This was also shown in an undergraduate paper by John Gemmer, now at Brown, who gave an explicit derivation of this dependence by solving some nasty integrals.
So, for "sharper" fields, we expect a certain critical angle dependence, with a known formula. For "softer" fields, we expect no critical angle (or, the angle is 180 degrees). What does the full picture look like? Performing my computation of this angle, I found that it agrees with the established predictions in both limits (sharp and soft), but in the middle there is a transition that is described by neither limiting case! The established answer was wrong, and I was going to prove it and find the right answer! It was an unsolved problem in physics that was obscure enough that nobody else knew about it and simple enough that I could solve it. This is what the savvy call "low hanging fruit."
The main difference between sharp and soft fields is that sharp fields have a gravitational potential that is infinite at the origin, and it makes sense to set the potential to be zero at infinity, while soft fields do not (they can have singularities in the field {e.g. n=0.5} or in the density {e.g.n=0}, but singularities in the potential are important here), and the potential can be set to zero at the origin. A reasonable hypothesis is that the Keam-Gemmer relation (which I will start calling the angle dependence...now) only applies to fields with a potential singularity (n>1) and there is no critical angle otherwise (n<1). However, this assumption is violated by my computations.There is a special case, when n=1, corresponding to a logarithmic potential that can neither be zero at the origin or at infinity. Physically, this is like a mass distribution which is everywhere juuuust not massive enough to collapse into a black hole. This was also examined by Tee, who figured that according to Keam-Gemmer the angle should be 180 degrees, but according to his best computational ability (this was 2000), it was 174 degrees. Published evidence of this law breaking down!
So I tried to solve the unsolved problem, to find an expression for the angle dependence that agreed with my computations. I tried, but was unable to do so. I am not a very good mathematician. Tee, Gemmer, and myself all use different geometry and notation to derive the brachistochrone, so I was attempting to find an expression for this angle with my formalism, unsuccessfully. I wanted to ask Gary Tee how he and Ron Keam did it, but I don't know if he's still alive. So I found Ron Keam's email and asked him if he remembered how he contributed to a footnote in 1998. Now retired, he kindly replied saying his notes may or may not be in a big stack of papers in his attic, and mused that mathematical research serves as an effective elixir of life. Then, I tried working through Gemmer's derivation to see if he had made any approximations or Taylor series cutoffs or anything like that in order to solve the integral. There was nothing of the sort, and I was eventually to re-produce his answer. So, even though I had found that the Keam-Gemmer relation broke down in certain cases, I could not prove it.
Finally, I emailed John Gemmer to see if he minded answering some questions about something he did six years ago. He quickly got back to me and I explained the situation, explaining my results, Tee's logarithm results, and how they fit in between the two limits, and my intuition on the problem. He agreed with my intuition and found my results surprising. Then, he cleared up the discrepancy. One of the conditions for the brachistochrone is that the path is horizontal at its deepest point, and he integrated brachistochrone curves with this condition at a point very close to the origin up to the surface, making the starting point smaller and smaller. This is in effect a numerical method of replicating his derived result, which is in the limit of having the deepest point at the origin. What he found was that even for very small initial radius 10-6, his computations agreed with mine, that the Keam-Gemmer relation broke down. However, with much more intense computation, going down to a 10-20 initial radius, he showed that if you make the calculation extremely accurate you will eventually recreate the Keam-Gemmer relation for sharp fields and the no-critical-angle solution for soft fields.
The unsolved problem that I was trying to solve did not exist, and I had lacked the computational resources to prove it. What of Tee's logarithmic counterexample? A close reading of his paper points out that he had gone down to 10-8 in initial radius to do the computation, and suspected that he could bridge those extra six degrees if he went further. I should have read that paper more closely instead of just getting excited about it. Overall, it was a fun little brain teaser that I set myself on, but it turned out that the unsolved problem was actually solved.
As part of my paper on falling through the centre of the Earth, I studied something called the brachistochrone curve. From the Greek for "shortest time," this is the curve that allows something to fall from point A to point B in the least amount of time. Finding this shape was posed as a challenge by Johann Bernoulli in 1696 to the leading physicists of the day, and was quickly solved by Isaac Newton, Gottfried Leibniz, and others. The solution is a shape called a cycloid, the shape traced out by a rolling circle. Apparently Albert Einstein likes to ride them, and it is the fastest shape because it has the right balance of short distance and high speed (the cycloid with the green ball wins, ignore yellow and blue).
The brachistochrone curve inside the Earth (assuming uniform density) was worked out, among others, by Venezian around 1966. The problem is more complicated because gravity now varies (linearly) with distance from the centre, and the geometry is polar rather than Cartesian. The solution is the related hypocycloid, traced by a smaller circle rolling inside a bigger circle.
Another problem that had been worked out in the literature was the brachistochrone problem around a point-mass in Newtonian gravity: polar geometry where the gravitational field decays as 1/r2. This was solved independently by a few researchers, and there isn't an analytical solution (one that can be written down as an equation), but these curves generally run deeper than the hypocycloid, because gravity is comparatively stronger towards the centre, so they can save time by going deeper. What's interesting, however, is that if two points on the surface are separated by more than 120 degrees, no such curve exists. Beyond this, it is faster just to go "down" to the centre, switch directions, and go "up" to another point, rather than taking a smooth curve. If you try to calculate the brachistochrone curves, they hit a wall, so to speak. (that image is from John Gemmer, one of the people to figure this out. His website on the problem has some neat animations.)
Because the Earth is not uniform, and is not a point-mass, I developed a model to find the brachistochrone between any two points on a sphere, with an arbitrary gravitational field inside, which is where this story begins. Ultimately this model allowed me to calculate the brachistochrone through the realistic Earth, but that is not what this post is about.
I wrote a script that would generate these curves, going from their point of maximum depth to the surface. (For those that care, it is this equation, where alpha is -n and Rd is the deepest radius, 0.5 in the gif below. It is solved with the Euler method.)
 |
| Finding the fastest path by starting at the bottom, working towards the top [while satisfying the minimization conditions]. |
As the starting point got deeper and deeper, the curves tended to get straighter, which makes sense: the fastest way through the centre of the Earth is a straight line.
 |
| Generating brachistochrones in a uniform Earth, getting deeper and deeper. The longest paths are almost straight lines. |
 |
| Generating brachistochrones around a point mass. The curves do not connect points separated by more than 120 degrees. They hit a wall as you go deeper. |
It turns out, I was. Two publications had mentioned the power-dependence of this critical angle. One was by Kiwi NASA mathematician Gary Tee, who started working on problems like this after the Apollo missions. In a footnote of one of his papers , Tee mentioned that a coworker, Ron Keam, had shown that as a function of field exponent, the critical angle is 2π/(n+1), meaning that for n=2, the critical angle is 2π/3, 120 degrees as expected. This was also shown in an undergraduate paper by John Gemmer, now at Brown, who gave an explicit derivation of this dependence by solving some nasty integrals.
So, for "sharper" fields, we expect a certain critical angle dependence, with a known formula. For "softer" fields, we expect no critical angle (or, the angle is 180 degrees). What does the full picture look like? Performing my computation of this angle, I found that it agrees with the established predictions in both limits (sharp and soft), but in the middle there is a transition that is described by neither limiting case! The established answer was wrong, and I was going to prove it and find the right answer! It was an unsolved problem in physics that was obscure enough that nobody else knew about it and simple enough that I could solve it. This is what the savvy call "low hanging fruit."
 |
| I'll call it the Klotz Gap and minstrels will sing its praise. |
So I tried to solve the unsolved problem, to find an expression for the angle dependence that agreed with my computations. I tried, but was unable to do so. I am not a very good mathematician. Tee, Gemmer, and myself all use different geometry and notation to derive the brachistochrone, so I was attempting to find an expression for this angle with my formalism, unsuccessfully. I wanted to ask Gary Tee how he and Ron Keam did it, but I don't know if he's still alive. So I found Ron Keam's email and asked him if he remembered how he contributed to a footnote in 1998. Now retired, he kindly replied saying his notes may or may not be in a big stack of papers in his attic, and mused that mathematical research serves as an effective elixir of life. Then, I tried working through Gemmer's derivation to see if he had made any approximations or Taylor series cutoffs or anything like that in order to solve the integral. There was nothing of the sort, and I was eventually to re-produce his answer. So, even though I had found that the Keam-Gemmer relation broke down in certain cases, I could not prove it.
Finally, I emailed John Gemmer to see if he minded answering some questions about something he did six years ago. He quickly got back to me and I explained the situation, explaining my results, Tee's logarithm results, and how they fit in between the two limits, and my intuition on the problem. He agreed with my intuition and found my results surprising. Then, he cleared up the discrepancy. One of the conditions for the brachistochrone is that the path is horizontal at its deepest point, and he integrated brachistochrone curves with this condition at a point very close to the origin up to the surface, making the starting point smaller and smaller. This is in effect a numerical method of replicating his derived result, which is in the limit of having the deepest point at the origin. What he found was that even for very small initial radius 10-6, his computations agreed with mine, that the Keam-Gemmer relation broke down. However, with much more intense computation, going down to a 10-20 initial radius, he showed that if you make the calculation extremely accurate you will eventually recreate the Keam-Gemmer relation for sharp fields and the no-critical-angle solution for soft fields.
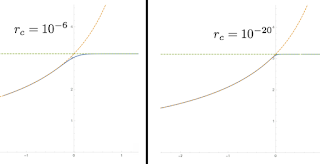 |
| The Klotz Gap vanishes. Thank you to John Gemmer for generating and giving me permission to use these images. |
The unsolved problem that I was trying to solve did not exist, and I had lacked the computational resources to prove it. What of Tee's logarithmic counterexample? A close reading of his paper points out that he had gone down to 10-8 in initial radius to do the computation, and suspected that he could bridge those extra six degrees if he went further. I should have read that paper more closely instead of just getting excited about it. Overall, it was a fun little brain teaser that I set myself on, but it turned out that the unsolved problem was actually solved.
Monday, 10 August 2015
Subscribe to:
Posts (Atom)