The Knot Untying Spectrum

I recently investigated a fun little problem in knot theory, about what kinds of knots can be generated by partially untying a more complex knot. I got some interesting results before realizing that somebody else had already asked and answered the same question. I still think it's a neat problem, so I'll explain the background and how I went about investigating it. It might be useful to have a knot table open in another tab while reading this, and I apologize in advance for the terrible MSPaint graphics.

Left: A DNA molecule with a knot at multiple stages of untying, getting a bit longer with a smaller knot at each stage. Scale bar is 8 microns. Right: Diagram of the pathways that a 101 knot can take to untie (we do not expect the knot in the left image to be a 101, it is just an example).

This was motivated by my recent paper that I talked about here. In it, we discussed observations of DNA knots that partially untied into smaller knots, implying the original knots were sufficiently complex for this to happen. We also ran numerical simulations of a 101 knot  untying, and found that it could either untie completely or in multiple stages, becoming an 81, 61, and 41 (figure-eight) before untying.

A knot unties in two stages at the right side of this stretched DNA molecule, leaving a smaller intermediate knot after the first stage. For what kinds of knot is this mathematically possible?

Even though we don't know what kinds of knots I'm actually studying in my experiments, we know from several. different. measures. that they are very big and complex (by knot standards), so I was envisioning a simulation project where we look at the pathways of many different kinds of knots untying in polymers to determine the statistics of knot untying mechanisms. However, I realized that there was a more fundamental problem, which is that it's not trivial to figure out what kind of knot you get when you partially untie a bigger knot. Sure from looking at a drawing of a 101 knot you can figure out that it goes to an 81 knot, but try to tell me what kind of knot you get when you partially untie a (let's say) 10165 knot. So, I wanted to figure out what kind of knots can untie into other kinds of knots. There are many, many knots, but limiting my knot menagerie to 10 crossings or fewer gave me 249 knots to study and seemed like a good cutoff because it was small enough that I could wrap my head around it but large enough that I could get statistics.

Partially untying a 10165 knot gives you a new knot of (initially) unknown topology.

Knots are represented by diagrams, which are a two-dimensional projection of a three-dimensional entangled loop, where one section of a loop can pass over or under another. A lot of knot theory has to do with how these diagrams can be transformed into one another, with certain moves keeping the topology of the same (called Reidemeister moves) and others leading to a different kind of knot. Knots are typically labelled in Alexander-Briggs notation, which has a big number for the minimum number of times the knot diagram crosses itself, and a smaller number for the index of that knot within the set of knots with that many crossings. There isn't much pattern to the index number, except that for even crossings the first one is a twist knot, and for odd crossings the first is a (P,2) torus knot and the second is a twist knot. There is no deterministic way to know the type of knot given its diagram, but there are calculations you can do with a given diagram (call it A) that can be compared to the same calculation from a diagram of known topology (call it B), which gives evidence that diagram A represents knot B, but knowing this for sure is an open mathematical problem.

The mystery knot with over a dozen crossings has the same Alexander polynomial as the trefoil knot, which provides evidence that is in fact a trefoil knot (it is!).

One such calculation involves calculating the Alexander polynomial, where you label all the n crossings in a diagram and the n+2 regions that the diagram divides the plane into, and define an (n × n+2) matrix with values determined by how each crossing behaves next to each region, and take the determinant of a square subset of the matrix (see a better explanation on page 21 of this document). There are similar polynomials called Jones and HOMFLY*, but I like Alexander the best because it's my name (and also it tends to yield simpler rational numbers). The Alexander polynomial is used a lot in polymer simulation papers, where the chain is projected onto a plane, the Alexander polynomial is calculated based on that projected diagram, and the value at some point is compared to the known values of specific knots, to try to determine what kind of knot it is. This works well if you have reason to believe that all your knots are simple (for example when forming in an equilibrium polymer), but breaks down if you have a more diverse set of knots. For example, the 61 knot has the same Alexander polynomial as the 946  knot, and there are 11-crossing knots with the same Alexander polynomial as the unknot (for which the polynomial is a constant 1).

So, based on what I knew about this, my procedure for figuring what kinds of knots I get when I partially untie a bigger knot would be something like:

1. Partially untie knot.
2. Calculate Alexander polynomial
3. Compare to Alexander table.
4. Profit.

The question is, what is the mathematical operation equivalent to "pulling some rope out of the knot just a little bit and stretching it again"? This comes back to how topology is defined in simulations of open chains (which technically are unknotted because they aren't a closed loop). To calculate the topology, the chain is looped through "minimally interfering closure," which, if the ends are far apart and knot is in the middle, just means connecting the ends at infinity.  But if I open a closed chain, untie it a bit, stretch the ends really far apart and then reconnect them, I can skip the last step and just close it immediately after untying. So, this open-untie-close operation is equivalent to taking one of the crossings in a diagram and changing it from "over" to "under" or vice versa, which is known in knot theory as a crossing switch. A topic of interest in knot theory is the unknotting number of a knot, which is the minimum number of these crossing switch operations that are required to untie a knot. One thing I like about this is that you can mentally picture the switch and then mentally schwoop out the now-non-essential parts of the knot to try to figure out how it evolves to a simpler knot. My mental schwooping only goes so far though.

The untie-and-pull operation of an open knot is better represented by the crossing-switch of a closed knot.

So all I had to do was take all 249** knot diagrams with 10 or fewer crossings, calculate the Alexander polynomial for each one, flip all 2,343 crossings, and calculate the Alexander polynomial for each new diagram. At this point it was clear that I should be doing this with some kind of algorithm, so I downloaded the knot theory package for Mathematica, which is maintained by a professor at the University of Toronto.

For each knot you can calculate something called a Dowker code (also known as Dowker-Thistlethwaite), which is an array of numbers representing the crossings of a knot diagram, with numbers that are positive if the crossing has the strand going over the other, and negative if it goes under. A crossing switch can be achieved simply by replacing the positive numbers with a negative or vice versa.

How to calculate a Dowker code. I can make it "untie" a little by switching one of the negative numbers to positive or vice versa.

So, I had my means of attacking this problem: iterate through every knot, iterate through every crossing, flip it, calculate the Alexander polynomial at some value, and save the results for later analysis. When I started doing this and looking at the results, one issue that arose was duplicates. I mentioned above that some pairs of knots have the same Alexander polynomial. For knots with 9 or fewer crossings, there were about a dozen of these pairs, many of which involve composite knots (two knots on the same closed loop), whose polynomials are the product of the prime knots that make them up. In many cases I was able to use the Jones polynomial to break the tie***, the one exception being the 912 knot, which has the same Alexander and Jones polynomials as the 41#52 compound knot. However, these duplicates were typically a nuisance but not an issue, because the duplicates typically had different crossing numbers and usually the lower one made sense but the higher one didn't (if I untie an 8 crossing knot and I get either a 6 crossing or a 9 crossing knot, I know it's the six crossing knot).

There are a few families of knots where it's simple to figure out what happens when they're partially untied. Twist knots, for example (like the 101, 81, 61, 41 in my first example) will untie into the unknot if their "clasp" is cross-switched, but will untie to a twist knot with two-fewer crossings if they are untied in their twisty section. Likewise, (P,2) torus knots will evolve into (P-2,2) torus knots when one of the crossings is flipped. I haven't been able to figure out a general principle for higher-order torus knots, although the simplest example (the 819 knot) can be partially untied into two trefoil knots as well as a 51 torus knot. It came as a surprise as me that a prime knot can be untied into a composite knot, although it makes sense when you look at the diagram.

Left: Highly symmetric (P,2) Torus knots can only untie into (P-2,2) torus knots. Right: The 819 knot can untie into two trefoil knots.

Most knots had multiple simpler knots they could untie into. At each crossing number, there was a distribution in the number of untying pathways that was approximately Gaussian. There was also a knot at each level that had the greatest number of untying pathways. More symmetric knots tend to have fewer pathways for intuitive reasons, the lowest being the (P,2) Torus knots that can only untie into (P-2,2). 62, 76, 814, 932 were all champions, while 10117, 10119, and 10147 all had eight untying pathways. There a few other things that can be done with this information, like looking at how the average number of pathways grows with the crossing number, or calculating the total number of knots that can be reached starting with a given one and untying it multiple times. I was somewhat interested in figuring out the greatest number of pathways that a given knot could take to untying, but never really got around to doing this. Another thing that might be interesting is to find the knot that must untie in the greatest number of stages (e.g. the 101 can take 4 steps to untie, but it can also take zero), however the answer this is probably just a (P,2) torus knot, which takes roughly P/2 steps to untie.

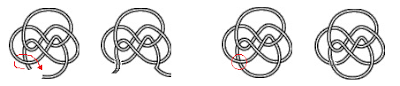
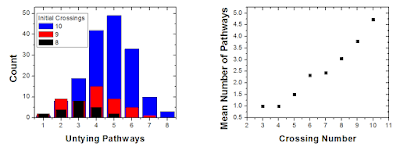
The 814 knot can untie in five different ways, and take 8 different paths to untie completely.

There was one result that I didn't understand, which is that apparently the 10161 knot could be untied into the 10145 knot. If this is real then there may be a family of knots that can be cross-flipped into knots with the same crossing number, if it's not real then there are flaws in my algorithm, but I can tell from known cases that it's not *totally* wrong.

Untying pathway stats with no real insight. Left: Histogram of the 8, 9, and 10 crossing knots and how many ways they can untie. Right: Average number of untying pathways as a function of crossing number. Is it linear?!

When breaking into a new field, it can be hard to do a proper literature review because you don't know the lingo. The closest thing I could find to what I was interested in was "knot adjacency," which was investigated by a few people who were interested in how knots were "n-adjacent" to the unknot, meaning they could be untied with a minimum n simultaneous crossing switches. However, after I got my results I did a bit more digging and found the term "Gordian distance," which lead me to a 2010 thesis that computed a table of "knot distance" between the prime and composite knots that I was investigating, all the knots that could be reached with a certain number of crossing switches from another knot. What I had done was essentially the one-flip subset of this. The application of this table was also DNA related, it was inspired by topoisomerase enzymes that can untie knots in DNA by passing strands through one-another. I was able to check my results against those in the table to verify I wasn't completely wrong in my conclusions.  A more recent paper, published in the Journal of Knot Theory and its Ramifications, spoke of knot fertility, defining parents and descendants based on crossing flips. They were interested in calculating the knots that can be cross-flipped into every single less complex knot. The most complex fertile knot they found was 76. There are definitely others interested in this problem, but there aren't enough of them that they've settled on a unified vocabulary.

I did go a bit further in some aspects than these other two papers, but I don't think that's enough to warrant a publication on it. One question that I think remains open and would be interesting if solved is to find a general form for the untying pathways of torus knots, beyond just the (P,2) variety. I have two data points for this: the 819 (the (4,3) torus knot), which can untie into either two trefoils, the 51 torus knot, or the 75 knot, and the 10124 knot ( (5,3) torus) which can be untied into 819, a compound 31#51, 942 and 947 (or their Alexander-sharers). Even from those two points there are patterns that emerge, but that's a bit too extrapolaty. Even though I wasn't the first to do this, it was still fun figuring it out.



*HOMFLY seems like a name a TV executive from the early 90s would make up for a rapper appearing on the show. However, it is named after the initials of six of its derivers.

**actually just 247 of them...the 31 and 41 knots obviously won't untie into anything smaller.

***no pun intended

Two new posts on PhysicsForums about DNA biophysics

Ahoy readers,
I've written two new posts on PhysicsForums summarizing some recently published papers on single-molecule biophysics. One is a summary of a paper I wrote, and one is more of a news-style article about another paper that I'm familiar with but wasn't involved in.

https://www.physicsforums.com/insights/new-research-on-untying-knots-in-polymers/

https://www.physicsforums.com/insights/using-the-spaghetti-twist-to-align-dna/

Applications of higher-order derivatives of position

One of the first things we learn in physics is that velocity is the rate of change of position, acceleration is the rate of change of velocity, and how to figure out the quantities you don't know based on the ones you do. Velocity and acceleration are important throughout physics because of velocity's part in momentum and kinetic energy and acceleration's role in Newton's law of motion. What we don't hear much about are the higher-order derivatives. Here, I'll briefly discuss these quantities and what they're useful for. For more detail than in this post, this paper summarizes a lot of the information and applies it to trampolines and rollercoasters.

Jerk-the third derivative

The rate of change of acceleration with respect to time is called jerk. In highschool, when I was dealing with a lot of acceleration based questions, I imagined that when I got to university I would start seeing jerk-based questions. I was wrong, they never come up. There is a lot of information on the Wikipedia page about jerk, more than I'll get into here.

Most applications of jerk relate to its minimization. Reducing changes in acceleration throughout a trip makes the trip for comfortable, and most engineering for "smoothness" of some sort deals with minimizing jerk. There are a lot of papers on this, many of them having to do with robotics. The challenge is figuring out which joints to move and when in order minimize the jerk of the payload.

There have been some papers published in the American Journal of Physics and related publications about the educational value of studying jerk, and in my paper on minimizing relativistic acceleration, we left jerk minimization as an exercise for the reader.

Snap, Crackle, and Pop (4th, 5th, and 6th derivatives).

The derivatives of jerk are sometimes called, respectively, snap, crackle, and pop. In searching for the origin of these terms (obviously they're taken from the Rice Crispies characters, but the origin of their use in physics), I found a reference in a 1997 paper that stated:

These terms were suggested by J. Codner, E. Francis, T. Bartels, J. Glass, and W. Jefferys, respectively, in response to a question posed on the USENET sci.physics newsgroup.

Doing some sleuthing and getting into weird old internet stuff, I found the current iteration of that newsgroup, which has a lot of John Baez arguing with crackpots, and the thread being referred to may be here. Doesn't quite explain the origin though. They may have just been invented by John Baez.

Whereas jerk tends to be something that is minimized to ensure a smooth trajectory, snap tends to be used for predictive motion. Predicting the motion of wrists for prothetics, of quadcopters for interception, and of cats' eyes when they're watching videos. There was a paper examining the snap of the cosmological scale factor, which may be one of its most fundamental uses.

Crackle is rarely used (based on a literature search), and when it is it again tends to be in predicting human motion. Pop is similar, there is very little written about it (besides "it's called pop!") except for an engineering paper again about predicting motion. Less applied, in the world of physics there is this paper, on integrating the N-body program defines kinematic variables all the way down to pop in its algorithm.

After that, there has been nothing written about the seventh derivative, one paper about using the eighth derivative for satellite orbits, nothing for ninth or tenth, and a 1985 MIT internal memo about AI and eye tracking that mentions the eleventh derivative as an example. I think that is the bottom turtle.

Absement: the Integral of Position

The integral of position is called absement for some reason. If you spend one second standing on a one-meter stool, you will have gained an absement of one meter second. Gas pedals in cars function with absement in mind, your speed depends on how far you depress the pedal and how long you keep it down. There is a musical instrument called a hydraulophone which looks like several adjacent water fountains, and sound is produced when someone pushes down on one of the streams. The tone produced is proportional to how far and how long the stream is depressed. In fact, I would semi-seriously argue that the whole concept of absement just exists to describe hydraulophones and vice versa. There is a big explanation on Wikipedia about how there are higher integrals like "absity and abselleration" and an integral of energy called actergy, but I'm pretty sure someone just made these up on a whim sort of like those weird animal plural names like "a parliament of owls." There are two names, Mann and Janzen, that repeatedly come up when searching these things, so I suspect those are the main promulgators of these words.

Traversing the Six Gaps of Hell

[This was written in July 2017 for the MIT cycling team blog. The guy I sent it to left MIT shortly after and it was never uploaded, so I am posting it here. Also, it's not about physics]

"Yesterday" I, along with 15 other riders from the MIT cycling club, rode the Six Gaps ride through central Vermont. It was 130 miles long and featured six extremely arduous climbs through mountain passes. It was a great experience and one I hope to never repeat any time soon.

Strava link #1: https://www.strava.com/activities/1096905818

Strava link #2: https://www.strava.com/activities/1096828371

We drove up from Cambridge and stayed at the Swiss Farm Inn in Pittsfield, had a brief pow-pow before going to bed, and woke up at 5:30 to enjoy their proclaimed World's Best Breakfast, then drove to a nearby school to park the cars and head out/up on the bikes. I had initially planned to do only four of the gaps, but after climbing the first one and not feeling dead, I elected to ride all six. This was by far the longest ride I had ever done; I was riding in miles what my previous longest ride was in kilometers. Because I was pushing distance and pushing height to the extreme, I didn't want to also push speed, so stayed back from the main group of crazy people with Ethan and Roger. After each gap we stopped at a general store to refill our water bottles and get refuel, usually arriving when the front group was departing.

The ride was very clearly characterized by its constituent gaps, and I  will describe each of those. The flats in between each gap were nice but not all too memorable, lots of farmland with pretty mountains in the distance. The roads were in good condition with very few potholes, the drivers in general were not jerks and gave us space while passing. There were more encouraging thumbs-up and waves from cars than there were aggressive honks.

My Strava is in metric, deal with it.

Gap #1: Brandon Gap

We parked in between Rochester Gap and Brandon Gap, in a location carefully chosen by Brian to be at the bottom of a hill. We set out at about 7:30 and quickly came to Brandon Gap. We agreed to do this one no-drop so we could get a sense of which riding buddies would be appropriate. This climb was totally unpaved, which I was not really prepared for. It was gravel with a few tire-track lines of less-gravel, that each of us followed up. In terms of grade and altitude this was probably the easiest climb (although I'm perhaps biased by the fact that it was first) but the gravel made it a tad dicey. Fortunately the downhill was paved, and this was one of the fastest descents I had ever done: it was 4.5 miles and took 9 minutes, and I was breaking to avoid hitting turns too fast.

After this the groups naturally formed, with groups of three different speeds doing all six gaps, and one group doing four gaps.

The Pow-Wow

Gap #2: Middlebury Gap

This was perhaps the longest and highest gap, but also the least steep, so it was manageable. I don't have a bike computer, so every time we got to a local maximum I'd ask my ride-mates if we were at the top, and every time they'd laugh and say no. I was starting to realize what I was getting myself into, that these gaps were more than an extended Eastern Avenue. The ride up Middlebury was pretty with a few small towns along the way.

Gap #3: Lincoln Gap

This was, objectively, the worst gap. It started out as a manageable climb with some occasional unpaved parts. Then, instead of pointing forward, the road pointed up.  For 2.5 miles the road had an average grade of 14%, at times reaching 24%. I don't even know that's possible because I feel like the asphalt would just slide down the hill before it could set. 2.5 miles doesn't seem very far but it is when you can't exceed 4 mph. Each of us eventually stopped biking and started walking; the combination of strength, endurance, and gear ratios had failed. First I started doing the paper-boy and swerving back and forth to lessen the gradient. Then I started standing up and using my weight to force each pedal stroke down, until this failed as well.  Loading up the cars at MIT I noticed that Daniel, who normally rides a carbon Cervelo, had brought his clunkier commuting bike because of its more favorable gearing. On Lincoln gap, I understood why. The road up Lincoln was narrower than the others, and had a lot of shade from forest lining both sides. Eventually the road levelled out enough for me to get back on my bike, and I made it to the top where there were lot people who had driven up to hike. The way down was unpaved, which was pretty sketchy given how steep it was, so I basically squoze the breaks the entire time.

Gap #4: Appalachian Gap

I was going to say that this was one of the more challenging ones, but who am I kidding, they were all extremely challenging. It had a fairly comfortable "are we there yet"-inducing foothill through some farmland, then a big descent before the climb proper started. This one was a fairly winding road up the mountain, such that you couldn't really see what coming around the bend, whether it was a mild lessening of slope or whether you were about the face a wall. The average grade of the climb-proper was 9%, with a mile straight at over 10%. At this point I had exceeded my previous distance record but was feeling pretty good, and decided to power up the top. Eventually I rounded a corner and could see the next two curves leading to the gap at the summit, which was an encouraging sight that gave me a boost to the top. This one was probably my favorite. I don't remember much about the descent, so it was probably uneventful.

Gap #5: Roxbury Gap

We had put in like seven hours of riding by the time we got to this one, and I was starting to feel fatigued. It was fairly similar to the Appalachian gap, turny and steep, except perhaps a little bit steeper. If I had done this earlier in the day I would have had a better time at it, but as it stood it was a bit too much to handle so I took a break and walked it for a bit before getting back on the bike and summiting. Towards the top and about 94 miles into the ride, my Garmin watch died, so I switched to phone stravving for the rest of the ride. The descent was unpaved and also had some extreme washboarding going on, so it was a bumpy ride despite my vigorous braking. Right at the bottom there were two kids with a lemonade stand, which we all gladly patronized.

Gap #6: Rochester Gap

The last gap! We got here around 6 PM, and 11 hours after setting out I was ready for this to be over. This was probably the easiest paved climb in terms of length and steepness, but I was not in the same condition I was in in the morning. I down-shifted and set to peddling, but noticed I was falling behind my ride buddies. I realized this was not because of fatigue per se, but because my ass was so sore that it hurt to stay in the saddle, so I did a lot of this climb standing up and pumping, finding a reserve of strength as I paper-boyed my way to the top. There was a sign marking the gap, which was a welcome sight. Right when I summited it started raining, and we rolled down the last descent into the Rochester school parking lot, and it was over.

I think overall I performed as well as I could have given how arduous this ride was; my bike worked well the whole time and neither my body nor my mind failed. I had a Clif bar at the top each peak and kept as well-hydrated and electrolyted as I could, which kept me going for the twelve hour journey. I only decided to do the trip a fortnight prior and didn't put in any specific training, but there are a few things  I might do differently. I would try to get more appropriate climbing gears on my bike (I forget what my ratio is but it's not good), I would practice more on steep hills like School St in Arlington, and I would try to lose some weight so I'd have less to haul up. This was a really fun but extremely difficult ride; I don't regret doing all six instead of a truncated four. I recommend doing this once, but only once.

Extreme High-Speed Dreidel Physics

(Warning: if you're viewing this post on a phone with limited data...you should probably leave before all the gifs load)

Every November or December, Jews around the world celebrate Hanukkah, a holiday that commemorates defeating and driving out the Hellenistic Seleucids from Israel and establishing the short-lived Hasmonean kingdom* around the year 160 BC. The celebration of Hanukkah involves lighting candles, eating greasy food, exchanging gifts, re-telling the story, and playing games with a spinning dreidel.

Legend has it that when the study of Judaism was banned by the Seleucids, scholars took to the hills to study in secret, and when authorities came to investigate, they pretended they were just doing some good wholesome gambling. That legend, however, is very likely made up and doesn't appear in print before 1890. I read an article arguing that the dreidel originated from a popular gambling device called a teetotum that was popular in Northern Europe in the medieval period, that eventually made its way into Yiddish culture. The letters on the four sides of the dreidel (equivalent to N, G, H Sh) are interpreted to stand for the Hebrew "Nes Gadol Haya Sham" (a great miracle happened there), but originally stood for the Yiddish rules for gambling with a dreidel: nit (nothing), gants (everything) halb (half), and shtel ein (put one in)**.

From a physics perspective, a dreidel is an example of a spinning top, a source of extremely difficult homework problems in undergraduate classical mechanics related to torque and angular momentum and rigid body motion and whatnot. I was chatting with a theorist I know who mentioned that it would be fun to calculate some of these spinning-top phenomena for the dreidel's specific geometry (essentially a square prism with a hyperboloid or paraboloid base), and I suggested trying to compare it to high-speed footage. A quick literature review revealed that most of the dreidel analysis has to do with whether the gambling game is fair and how long the games last. Annoyingly, the search was obfuscated by the fact that there's a publisher called DReidel.

My lab has a high-speed camera that is used to film gel particles and droplets as they deform. It is normally connected to a microscope, but with the help of a student in my lab, we removed it and connected it to a macroscopic lens we had lying around in ye-olde-drawer-of-optics-crappe. A representative of MIT Hillel graciously provided me with a few dreidels, and I some time spinning the dreidels in front of the high-speed camera and recording them at 1000 frames per second.

Before I get into the more quantitative analysis, let's just take a look at what a dreidel looks like in slow motion, because as far as I can tell from a the google, I am the first person to attempt this.

As I initially spin the dreidel, it spins in the air a few times, lands with an axial tilt, and gradually rights itself as its angle of precession comes closer to the vertical. After that, you can see it spinning rapidly and precessing a little bit, but not doing anything too crazy.

The self-righting behaviour is a lot more extreme when I do the advanced-level upside-down flip.

On those first few bounces, it really looks like it's going to fly out of control and crash, but still it gradually rights itself into a stable rotation. While this self-righting tendency is strong...it is not unstoppable.

It's also pretty fun to watch what happens when they eventually lose stability and fall over.

This self-righting is too complicated-looking for me to understand right now, so let's look at something simpler: the steady-state (a) rotation and (b) precession.

It rotates several times while precessing from left to right.

To perform quantitative analysis of the dreidel's motion, I would want to be able the measure the phase of its rotation over time. Because the dreidel is made of reflective plastic, as it spins it reflects light into the camera, moreso when its face is parallel to the plane of the camera. Thus by measuring the total intensity, we should have a proxy for the phase of the dreidel, each intensity peak being a quarter-turn, and can investigate how that evolves over time. I wrote a MATLAB script that summed the total intensity of each frame and plot it over time.

There was initially a problem with this method of analysis, however. You can figure it out if look at the wall behind the dreidel in the above gifs (especially the wide crashing one), and notice that it's flickering. This is because the room is illuminated with AC electric light with a 60 Hz frequency. The light intensity is proportional to the square of the current, so it has a maximum twice per cycle, and the light flickers at 120 Hz. That is exactly the frequency at which the intensity fluctuates; the flickering was swamping the contribution from the dreidel. However, the quarter-turn frequency isn't that far off, so I was getting some neat beat frequency dynamics as well***.

This caught me off guard and it was skewing all my videos, so I took another few recordings using my cell phone flashlight with all the AC lights turned off. The videos don't look nearly as good, but the time-series are cleaner.

We can the intensity fluctuating periodically every ~8 ms, corresponding to a rotation period of 32 ms (nicely close to the square root of 1000, so it's also around 32 rotations per second), and a slower mode of about 200 ms or 5 precessions per second. 32 rotations per seconds is 128 quarter-rotations per second, so you can figure out why it took me a while to figure out that I had to disentangle it from the 120 Hz light flickering.

The fourier transform shows two peaks, one corresponding to rotation and one to precession, which is of stronger amplitude (I believe this is due to my analysis method and not to actual physics). The reason the peaks are smeared and not as at a sharp frequency is because the angular velocity gradually decreases as the dreidel loses energy to friction, so the peaks get smeared to the right.

With the flickering out of the way, I can also calculate how the rotation period evolves over time, using a peak-finding function in MATLAB. It gradually gets slower, as expected, which 6-7 ms between peaks at the beginning, and 14 ms between the peaks before it crashes. If this is caused by dry friction at the base, we would expect the frequency to decrease linearly with time. If it's caused by viscous drag, we would expect an exponential decrease. What do we see? The fact that it's discretized by the frame rate makes it harder to tell, but applying a rolling average on the frequency decrease suggests that it is linear and thus caused by dry friction.

The measurement gets a bit hairy towards the end.

That was mostly a discussion of the rotation, although precession presented itself as well. Let's take a closer look the precession. I wanted to measure the angle the dreidel was at with respect to the vertical, and how that evolved over time. This is not as easy to measure as the total image intensity; I had to use Principal Components Analysis. I found an algorithm on this blog post, and it worked as follows:

1. Define a threshold intensity such that everything in the image above the threshold is dreidel, and everything below it is background. Set the dreidel equal to 1 and the background equal to 0.
2. Define two arrays, one containing all the x-coordinates of all the 1's, and the other containing all the y-coordinates of all the 1's (such that each 1-pixel is represented in the array).
3. Calculate the 2x2 covariance matrix of the location array.
4. Find the eigenvectors and eigenvalues of the covariance matrix.
5. Find the angle associated with the eigenvector with the larger eigenvalue (e.g. the arctangent of the ratio of its components)

With some finagling to get the angle in the correct quadrant (I wanted the angle from the vertical, not from the horizontal), this works pretty robustly. It works better if I crop the movie to only include the stem. This actually only measures the angle of the dreidel projected onto the plane of the camera and doesn't provide information about its tilt towards or away from the camera, but it's good enough to see how the precession angle evolves. I can examine how the angle evolves over time...and it's pretty neat.

Two things are apparent from looking at this graph: both the amplitude and frequency of precession are increasing over time. The fourier spectrum of the precession angle contains only the precession peak, without the rotation peak at higher frequency. What's happening is that gravity is exerting a torque on the dreidel at an angle relative to its principal angular momentum vector, which induces a precession in the direction determined by the cross product of spin and down. The angular frequency of precession is inversely proportional to that of rotation, so that as the dreidel slows due to friction, its precession speeds up, which is what we see. The spinning is essentially preventing the gravitational torque from pulling the dreidel down, and as it loses angular velocity, the precession angle gradually increases.

This whole project started as a discussion with a colleague about how the term "Jewish physics" should be repurposed from a label the Nazis used to discredit Einstein, and dreidels seemed like a natural thing to focus on. After fiddling around with a high-speed camera for a bit I got some cool videos, and thought I'd share them. I didn't really cover anything in this post that isn't explained in great detail in dozens of analytical mechanics textbooks, but it's perhaps the first time anyone has used a high-speed camera to record a dreidel. I thought it was neat.

In addition to being a fun little diversion, it also spurned an improvement in my DNA image analysis code. It was taking so long to open the dreidel movies in MATLAB that I looked into a more efficient way of doing so, which improved loading time by like a factor of 20 (from 55 seconds down to 3 seconds), which I now use to open DNA movies as well.

*If you grew up hearing the Hannukah story every year, you probably will not recognize the words Hellenistic, Seleucid, or Hasmonean.

**For those unfamiliar with Jewish linguistics, Hebrew is a Semitic language related to Arabic and Ethiopian (Amharic), whereas Yiddish is a Germanic language that uses Hebrew letters, so some of the words are similar to the also-Germanic English, e.g. halb and half.

***This is what the FAKE NEWS wrong analysis looks like:

Comfortable Relativistic Space Travel: New paper on arXiv

I have written a new paper which has just come out on arxiv.org. It has the somewhat long title of  "Relativistic minimization with constraints: A smooth trip to Alpha Centauri" and can be found here. My co-author on this paper was Riccardo Antonelli, who also writes a physics blog, called Hologrammata. It discusses and derives the most comfortable way to plan a relativistic journey, which may become relevant in several thousand years when we can actually go fast enough for this to matter.  In this post, I will explain what this paper is about and what inspired me to write it.

Artist's impression.

Every month, the American Journal of Physics puts out a new edition with about twenty articles. These are usually a delight to read and can be read by anyone with a basic physics background. Some of the articles are about physics education, but most of the research articles involve applications of established physics to problems nobody had quite thought of before. (This is where my tunnel-through-the-Earth paper is published).

In the October 2016 edition, I read an article called "The Least Uncomfortable Journey from A to B" (possible free version here) by three Swedish and possibly French researchers, Anderson, Desaix, and Nyqvist. In it, they ask the following question: on a linear trip taking time T from point A to point B separated by distance D, what is the trajectory (instantaneous velocity as a function of time or distance) that minimizes the  time-integrated squared acceleration? If you can't mentally convert that sentence into LaTeX, the "discomfort" here is the total acceleration that the passenger feels throughout the trip, pushing them into their seat on the first half of the trip, and thrusting them out of their seat on the second half.

The solution, which they find through Lagrangian-style variational calculus, turns out to be a trajectory with constant jerk, where the acceleration decreases linearly over the entire trip, such that the velocity is a quadratic function of time. A lot of the paper talks about various analytical approximation methods, and also computes an alternate "least uncomfortable" trajectory where the squared jerk is minimized instead of the squared acceleration.

The interesting thing about the solution is that there is only one. The relative velocity (v/vmax) as a function of the relative position (x/D) or time (t/T) does not actually depend on the distance or time. No matter how far or fast you want to go, there is only one set least-uncomfortable way to get there. However, there is a problem with this. If you want to calculate how to plan a train ride that covers 500 miles in an hour, the solution is fine. But if you want to plan a trip that goes from Earth to Jupiter in an hour, then it starts running into some problems. Although it wasn't stated in the paper, the solution only holds when D/T is  much less than the speed of light. I was curious about finding a relativistic solution to this problem, and if I get curious enough about a problem that is actually possible to solve, I can be quite persistent.

In the relativistic version of this problem, when you consider the integral over time of the squared acceleration, it matters in which reference frame the time and acceleration are being measured. Because we care about the comfort of travellers and not of stationary observers, we consider the proper acceleration and not the coordinate acceleration. This problem can be formulated either in terms of "lab" time or proper time on the ship, there are benefits to both. My first attempt at this essentially involved following Anderson et al.'s derivation except with a lot of extra Lorentz factors, which is generally not a good way to go about things, and I stalled pretty quickly.

Then one day, I was talking to my internet friend Riccardo, who had just finished his master's thesis in string theory and holography. I figured a lot of the relativistic analytical mechanics formalisms might still be fresh in his mind, so I mentioned the problem to him. He too found the problem interesting, and came to the realization that if the problem was formulated in terms of the rapidity (the hyperbolic tangent of velocity relative to c) since its derivative is proper acceleration, it could be expressed as a much neater problem than my "add a bunch of Lorentz factors" approach.

The way to derive the solution, Riccardo discovered, is to treat it as a Lagrangian function of the rapidity rather than the position (such that you write down L(r, $\dot{r}$, ) instead of L(x, $\dot{x}$) and apply the Euler-Lagrange to higher-order derivatives of position than normal). Even though we were unable to derive a closed-form solution, it turns out, the rapidity of the least uncomfortable solution evolves like a particle in a hyperbolic sine potential, and I was able to generate solutions using the Runge-Kutta algorithm, which has been serving me well since I learned how to use it in 2008.

As I said, there is only one classical solution, it is universal for all distances and times. However, when relativity it taken into account, the solution depends on how close to the speed of light it gets: there is now a single free parameter that characterizes the solution, and we can express it in terms of its maximum velocity, rapidity, or Lorentz factor. Our solution recovers the classical solution in the low-velocity limit (which is good, otherwise we'd be obviously wrong), but as the maximum speed increases, a greater fraction of the time is spent close to the maximum (which makes sense, as the path is some form of "accelerate close to light speed, decelerate down from close to light speed" and as you approach light speed, your velocity changes less and less)

A figure from the paper showing relative velocity as a function of relative time. The classical solution is the inner parabola with the car next to it, the solutions get faster as you go out, the fastest has a maximum Lorentz factor of 100 and is marked by a rocket. While making this figure I had a minor legal quandary about the copyright status of unicode emojis.

Now, we had solved the problem that I was inspired to solve, the relativistic version of Anderson et al.'s least uncomfortable journey. However, this whole thing may be moot for space travel: you don't necessarily want to keep acceleration to a minimum, instead you might want to contintually accelerate with Earth-like gravity for the first half of the trip, then reverse thrust and decelerate with Earth-like gravity for the second half, so that the entire ride (besides the switcheroo in the middle) feels like Earth. We calculated a trip like this to Alpha Centauri, which would take six years relative to Earth and 3.6 proper years on-board due to time dilation, reaching 95% light speed. With our solution, covering that distance in the same proper time would only reach 90% the speed of light, and might be more appropriate for sending mechanically sensitive electronic probes or self-replicating machines than it would be for sending people.

Anyway, we wrote up the paper and now it's online for the world's reading pleasure. It was fun seeing this paper go from a persistent idea to a finished product in a few weeks time, and dusting off some of the long-forgotten special relativity tools. It was a nice little collaboration with Riccardo, where I came up with the problem and he came up with the solution. This is the first random physics idea I've had in while that has actually come to fruition, and I hope there are many more to come.

New article on the early history of science

I wrote an article on the first science experiments, over at PhysicsForums. Check it out!

Empirical Searches for Nominative Determinism

Nominative determinism is the idea that a person's name influences their life or career. The Seven Dwarfs are an example, and humorous lists have been written about people with names that suit their vocation. The world's fastest man is named Bolt, there was a Russian hurdler named Stepanova, a meteorologist named Julie Freeze, and eugenics pioneer Eugen Fischer. Considerable attention is given to a urology paper by Weedon and Splatt.

To my knowledge, the idea is not taken too seriously. However, I was recently curious about the extent to which people have looked for evidence of nominative determinism. I went on Google Scholar and found some results which I'm sharing with you now.

Most analyses of nominative determinism focus on medical professions, looking at whether specialists tend to have names associated with their speciality.

Examples of nominative determinism in medical research, with statistics of N=1. Ref.

Although this study was not entirely serious, it had a number of methodological flaws as it failed to consider the prominence of each surname in the medical fields relative to its prominence in the population at large.

One recent study was by four members of a family surnamed Limb, all doctors (two of whom named C. Limb are avid climbers). They surveyed a directory of over 300,000 medical doctors grouped by speciality, and went through the list and independently noted which were suited to medicine in general and to their speciality. The lists were then merged by consensus. They found that 1 in 149 doctors had medically appropriate surnames, and 1 in 486 had names relevant to their field. They noted:

"Specialties that had the largest proportion of names specifically relevant to that specialty were those in which the English language has provided a wide range of alternative terms for the same anatomical parts (or functions thereof). Specifically, these were genitourinary medicine (eg Hardwick, Kinghorn, Woodcock, Bell) and urology (eg Burns, Cox, Dick, Koch, Cox, Balluch, Ball, Waterfall). Some terms for bodily functions have been included in the frequency counts but are not mentioned because they are colloquial terms that may lower the tone of this publication."

Another study looked at nominative determinism in patients rather than doctors, trying to see if surname influences health. Based in Ireland, the authors looked through the Dublin phone book to estimate the percentage of people surnamed Brady (0.36%), and then tried to ascertain what fraction of them had been diagnosed with bradychardia (slow heart rate). The only data they had available was for pacemaker implants, and found that 8 out of 999 pacemakers had gone to people  named Brady. Despite the small numbers, this was statistically significant (p=0.03) relative to Brady's prominence in the Dublin telephone directory. The authors don't speculate on the causes of this, but neglected to discuss the idea that doctors may be subtly biased towards diagnosing Bradys with bradycardia.

"This increased bradyphenomenon in Bradys could be attributable to increased levels of bradykinin"

In the analysis of particle physics experiments there is something called the "look elsewhere effect" where any significant effect has to be considered in light of all the other effects that are being looked for (this xkcd gives an example of the folly), which reduces the overall significance of the interesting part. I suspect that if they had looked at what other surnames were over-represented in bradycardia diagnosis, the significance of Brady would be diminished. I think this proviso should be applied to any search for nominative determinism: look at the boring names as well as the silly ones.

There are a few other studies out there, mostly tongue-in-cheek. These do go a step beyond compiling humourous lists, but not too much further.